Part I
Introduction:
Many political arguments exist as to the cause of poverty in urban areas. The determined causes of poverty will influence the policies put in place for healthcare and other social welfare programs. A study was conducted on crime rates and poverty in a
certain town. The local news station
obtained data that claimed the crime rate increased as the number of kids that received
free lunches increased. To determine if
this claim is correct, a linear regression analysis was conducted on the data
to determine if the relationship exists or not.
Methods:
First, the data obtained from Dr. Ryan Weichelt of the
University of Wisconsin-Eau Claire in the form of an excel document was used to
create a scatter plot in excel with a trend line and corresponding
equation. Next, the data was inputting
into IBM SPSS Statistics 24 to run a linear regression analysis, a
statistical tool used to investigate the relationship between variables, which included the regression
coefficient (B), a number that shows how responsive the dependent variable is to the change in the
independent variable and the
coefficient of determination (R squared) that illustrates how much of the dependent variable is
explained by the independent variable. The scatter plot is pictured below in figure
1 and the results of the linear regression analysis are shown in figure 2. Finally, the results of the SPSS calculations were used to test the following hypotheses:
Null: There is no linear relationship between the percent of
kids receiving a free lunch (independent variable) and the crime rate
(dependent variable).
Alternative: There is a linear relationship between the
percent of kids receiving a free lunch (independent variable) and the crime
rate (dependent variable).
(Independent variable is the variable that explains the dependent variable and the dependent variable is explained by the independent variable).
(Independent variable is the variable that explains the dependent variable and the dependent variable is explained by the independent variable).
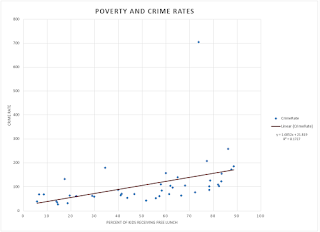 |
| Figure 1. Scatter plot of the percent of kids who receive free lunch and the crime rate. |
 |
| Figure 2. Model summary and hypothesis test results for percent of kids who receive free lunch and the crime rate. |
Results:
The scatter plot and the trend line show a positive relationship
between the percent of kids receiving a free lunch and the crime rate. The positive relationship is derived from the positive value of the slope, or regression coefficient. The regression coefficient indicates that for every one percent
increase in the amount of kids receiving a free lunch, the crime rate increases
by 1.685 percent. The low value of 0.173 for r2,
or the coefficient of determination,
in figure 2 indicates that the crime rate is weakly explained by the percent of
kids receiving a free lunch.
The significance level for the two-tailed t test at a 95%
confidence interval, shown in figure 2 is 0.005, thus the null hypothesis is
rejected that there is no linear relationship between the percent of kids
receiving a free lunch and the crime rate.
Finally, using the equation of the trend line, if a new area
in town was identified as having 30% with a free lunch, the corresponding crime
rate would be 72.375. I would not be
very confident in this result because although there is a linear relationship
between percent of kids with a free lunch and crime rate, the amount of
variation in crime rate explained by percent free lunch is very small as
indicated by the r2 value.
Conclusion:
The null hypothesis in this scenario was rejected,
indicating there is a positive linear relationship between percent of kids
receiving a free lunch and the crime rate.
However, the r2 value is very low so the variation in crime rate
explained by percent of kids receiving a free lunch is low. This indicates that there is another variable
or variables that explains crime rate better than percent of kids receiving a
free lunch. Technically, the news
station is correct, as the number of kids that get free lunches increases, so
does crime. However, this does not explain the crime rate very well, and these results could be misinterpreted so
I would be cautious about publishing these results to the public.
Part II
Introduction:
A major portion of public safety in an urban area is the responsiveness of the first responders. Because of this, the City of Portland, Oregon is concerned with adequate response times to 911 calls. To better serve the city, officials want to know what factors might explain where 911 calls come from. In addition, a local company is interested in building a new hospital in the area and they would like to know where to place their hospital. The best location of this hospital would be in an area that receives a high number of 911 calls. Thus these two questions would benefit from a study on the factors that explain where 911 calls originate from. The two questions answered in this section are as follows: determining what
factors might provide explanations as to where most 911 calls come from in
Portland, Oregon
and determining the best place to build a new hospital.
Methods:
First, data including number of 911 calls per census tract
in Portland, number of jobs, number of renters, and number of people with no HS
degree was imported to IBM SPSS Statistics
24. Then the dependent variable was set
to the number of 911 calls and the independent variables were set to the number
of jobs, number of renters, and number of people with no high school degree. An individual linear regression analysis was completed for each independent variable.
Then three scatter plots were created for each variable and the number of 911 calls in Microsoft Excel. Next, choropleth maps of the number of 911 calls per census tract, the number of renters per census tract, and a standardized residual map of the number of renters, which had the highest r2 value, were created. Residuals refers to the amount of deviation of each point from the best fit or regression line.The standardized residual map is a visual depiction of the standard deviation of these residuals. Finally, the results of the regression analysis were used to test the following hypotheses:
Then three scatter plots were created for each variable and the number of 911 calls in Microsoft Excel. Next, choropleth maps of the number of 911 calls per census tract, the number of renters per census tract, and a standardized residual map of the number of renters, which had the highest r2 value, were created. Residuals refers to the amount of deviation of each point from the best fit or regression line.The standardized residual map is a visual depiction of the standard deviation of these residuals. Finally, the results of the regression analysis were used to test the following hypotheses:
Null: There is no linear relationship between (number of
jobs, number of people with no high school degree, or number of renters) and
number of 911 calls.
Alternative: There is a linear relationship between (number
of jobs, number of people with no high school degree, or number of renters) and
number of 911 calls.
Results:
 |
| Figure 3. Scatter plot of the number of jobs and the number of 911 calls. |
 |
| Figure 4. Model summary and hypothesis test results for the number of jobs and number of 911 calls. |
The slope value shown in figure 3 states that for every job, there is an
increase of 0.007 in the number of 911 calls.
This positive relationship is determined from the positive
value of the slope (B value). The significance level for the hypothesis test of 911 calls and number
of jobs shown in figure 4 is 0.000 for a two-tailed 95% t test, therefore the null hypothesis is rejected
and there is a positive linear relationship between the number of jobs and the
number of 911 calls. The r2 value is 0.340, which is fairly
weak and suggests that jobs are not good at explaining the variation in the
number of 911 calls.
 |
| Figure 5. Scatter plot of people without a high school degree and number of 911 calls. |
 |
| Figure 6. Model Summary and hypothesis test results of people without a high school degree and number of 911 calls. |
The slope value in figure 5 states that for every person without a high
school degree, there is an increase of 0.166 in the number of 911 calls. This positive relationship is determined from the positive value of
the slope (B value). The significance level for the hypothesis
test of 911 calls and number of people without a high school degree is 0.000 for a two-tailed 95% t test, therefore the null hypothesis is rejected and there is a
positive linear relationship between the number of renters and the number of
911 calls. The r2 value is 0.567, close to 1 and
therefore the number of people without a high school degree explains a fair
amount (less than the number of renters but more than the number of jobs) of
the variation in the number of 911 calls.
 |
| Figure 7. Scatter plot of the number of renters and number of 911 calls. |
 |
| Figure 8. Model Summary and hypothesis test results of the number of renters and the number of 911 calls. |
The slope value states that for every renter, there is an
increase of 0.066 in the number of 911 calls.
The positive relationship is determined
from the positive value of the slope (B value). The significance level for the hypothesis test of 911 calls and number
of renters is 0.000 for a two-tailed 95% t test, therefore the null hypothesis is
rejected and there is a positive linear relationship between the number of
renters and the number of 911 calls. The r2
value is 0.616, close to 1 and therefore the number of renters explainss a good
amount of the variation in the number of 911 calls.
 |
| Figure 9. Choropleth map of the number of 911 calls per census tract in Portland, Oregon. |
 |
| Figure 11. Standardized residual map of the number of renters per census tract in Portland, Oregon with a potential hospital site. |
Figure 9 shows a choropleth map of the number of 911 calls per census tract in Portland, Oregon and has census tracts outlined in black that have more than 830 renters (highest category in figure 10). There are more calls in the central portion of the city than the outside census tracts shown by the brighter red colors in the center of the city. One can also see that census tracts with a high number of 911 callers also have a high number of renters, which supports the regression analysis completed earlier in figure 8. Figure 10 is choropleth map of the number of renters per census tract for the entire city of Portland, Oregon. Again, the areas with a darker green color indicate more renters and mirrors the brighter red colors in figure 9 with more 911 calls. In figure 11 the census tracts with
a bright red or bright blue color had a squared vertical distance value (from the trend line) that was substantially above or below the
regression line respectively (over or under-predicted). Specifically, these points had a larger or smaller number of 911 calls per increase in renters than the regression line predicted. On the scatter plot, these would be points that are very
high or very low compared to the regression line. For analyzing this data, the mean is 318, the median is 191, the mode is 80, and the standard deviation is 340. Outlined in black in figure 11 is a potential hospital site based on the highest deviation from the trend line.
Conclusion:
Overall three independent variables, the number of jobs, number of
people without a high school degree, and number of renters, were tested with the number of 911
calls as the dependent variable in census tracts in the City of Portland, Oregon. Of the three, the number of renters predicted
the most variation in the number of 911 calls with a coefficient of
determination of 0.616. Thus out of the
three variables tested the number of renters might provide the most explanation
as to where most 911 calls come from. In
fact, out of all the variables listed in the data, renters has the highest
coefficient of determination. From the data provided, the City of Portland can thus determine that the number of renters would provide the most explanation as to where the most calls come from. However the number of renters only explained 61.6% of the variation in the number of 911 calls, so further research would need to be conducted to determine the other variables that explain variation in number of 911 calls.
From this conclusion,
a company can also use the census tracts with the highest number of renters to
determine where to build a hospital. The
census tracts with higher numbers of renters would be ideal places to have a
new hospital built because the number of renters explains the most variation in
the number of 911 calls. Based on this,
the census tract with the highest standard deviation from the trend line, that
is the census tract with the most 911 calls based on the number of renters,
would be the ideal choice of location to build a hospital. This site is outlined in figure 11. However, this data is limited and it only 61.6% of the variation in number of 911 calls, so there are other variables that should be considered to make
a fully informed decision on where to put a new hospital. Other variables to be considered include road placement, the weighted mean center of the population, and correct zoning areas for a hospital.



No comments:
Post a Comment