Descriptive Statistics
Background and Definitions
When analyzing data, it is important to understand the different terms applied to data. Some of the more common terms include range, mean, median, mode, kurtosis, skewness, and standard deviation. Each of these will be defined in order to fully understand the results each term gives. Range is simply the highest value of a dataset minus the lowest value. Mean is the average of the values, that is taking the sum of all data points and dividing by the number of points. The median is the number that lies in the middle of a set of data. If there is an even number, then the middle of those two values is determined to be the median. The mode is the value in the data that occurs most frequently. Kurtosis is how flat or peaked (pointy) a data set is compared to a normal distribution that has a bell shape. a negative number for kurtosis means that the distribution is flat, or platykurtic and a positive number for kurtosis means that the distribution is peaked, or leptokurtic. Skewness describes how the symmetry of the data deviates from the mean of that data. If the skewness is 0, then the data fits a normal distribution. If skewness is a postive number the peak of the data is to the left, and if skewness is a negative number, then the peak of the data is to the right. Finally, standard deviation describes how dispersed data is around the mean. These terms were used in a case study of standardized test scores in two Eau Claire high schools.In Eau Claire, WI, there is a public perception that because Memorial High School has always had the student with the highest test score, the teachers at North should be fired. In order to test this claim, the above defined terms were calculated based on a sample of test scores from Memorial High School and North High School.
Methods
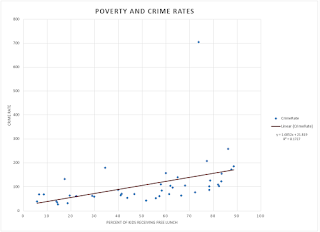
The range, mean, median, mode, kurtosis, and skewness were all calculated using Microsoft Excel. The standard deviation for each high school was done by hand in order to fully understand how standard deviations are calculated and what the number is describing in the data. The results are pictured below. |
| Figure 1. Range, mean, median, mode, kurtosis, and skewness for Eau Claire North High School calculated in microsoft excel. |
 |
| Figure 2. Range, mean, median, mode, kurtosis, and skewness for Eau Claire Memorial High School calculated in microsoft excel. |
 |
| Figure 3. Eau Claire North High School standard deviation calculated by hand. |
 |
| Figure 4. Eau Claire Memorial High School standard deviation calculated by hand. |
Results
After all calculations were performed, I do not think that teachers at Eau Claire North should worry about not having the highest test grade. Yes, according to the results, Memorial does have the highest test grade out of the two schools. In this regard, the data does support the public's claim. There are however several statistical analyses that show the performance of both high schools much better than just the highest test score, and in fact refute this claim by the public. The mean score of North and Memorial were 160.923 and 158.923 respectively. This shows that the average test score of North students is actually higher than Memorial, which means on average North students score higher than Memorial students. The median of North and Memorial, 164.5 and 159.5 respectively, supports that North has higher scores than Memorial. The mode of North and Memorial, 170 and 120, supports the mean as well. The kurtosis of both schools is mesokurtic, that is the data resembles a normal distribution (bell curve). The skewness of both schools is negative, which means both schools have high scores that push the peak of the data to the right. North's skewness value however is -0.579 while Memorial's is -0.185, showing that North has more high scores that are skewing the data more than Memorial's.Out of all the statistics, I think that the mean and median give the best indication that North does not perform worse than Memorial on standardized tests. The average of North was higher at 160.923 while Memorial had a mean of 158.538. The median of North was 164.5 while Memorial's was 159.5. Because the mean and median both have the same trend and are relatively close to each other, we can infer that there were no major outliers that would have distorted the mean in either direction. In both cases, North was higher than Memorial, which would imply that North performs better on their standardized tests overall. It is important to note however that the means of both schools are not hugely different, and thus the schools perform somewhat similarly on the tests.
Calculating Mean Centers and Weighted Mean Centers
Background and Definitions
Two other important statistical analyses are mean centers and weighted mean centers. Mean centers are the spatial equivalent of the average, or mean, of a set of data. It takes the average of all the x or y coordinates and divides by the total number of x or y coordinates to produce an average x and an average y coordinate, which together create one average point. A weighted mean center is the same concept, except x or y coordinates are multiplied by their frequency, or how many times they show up in the data and then divided by the sum of all the frequencies. This allows points that have duplicates to have more of an effect on data rather than having all points have equal effect.These two analyses will be used to determine the geographic mean center of population at the county level and the weighted mean center of population for 2000 and 2015 (weighted by population). These will be plotted on a Wisconsin county shapefile and then followed by a short discussion on trends seen from the data.
Methods
First, a previously acquired Wisconsin county shapefile was added to a blank map in ArcGIS. Then, a table with population data for each county in 2000 and 2015 was joined to the shapefile based on the GEO_ID field. The mean center tool was selected and first run without a weight to find the geographic mean center of population at the county level. The mean center tool was run twice more, with a weight of population in 2000 and a weight of population in 2015. Each point was clearly labeled and colored on a map with legend, north arrow, title, and sources. |
| Figure 5. Map of the geographic mean center and weighted mean centers with the population in 2000 and 2015 respectively. |
Discussion
This map shows that the mean center and weighted mean centers differ significantly in their location. The geographic mean center, as the name implies, lies in the middle of the state and is denoted by the blue circle. The weighted mean centers, both for the population in 2000 and in 2015, were located southeast from the geographic center and were denoted by the magenta and green dots respectively. The weighted mean centers are created by giving counties with a higher population a higher weight in the mean center analysis. In this instance, it is easiest to imagine that each person is a separate phenomena in the data and the number of people equates to how many times a 'dot' is recorded in the middle of the county. Thus the counties with a higher population have more frequencies within their boundaries, which gives them a higher weight.It makes sense that both weighted dots would be located southeast from the geographic center because the southeast part of Wisconsin holds most Wisconsin cities including Milwaukee and Madison, two of the largest urban areas in the state, giving Milwaukee and Dane County a very high population as opposed to other more rural counties. The weighted mean center in 2015 shifted slightly to the southwest. This could be caused by an increase in population in large urban areas in that direction, mainly Madison. Even with this slight shift, it is clear that the large urban area of Milwaukee and the surrounding area hold a large portion Wisconsin's population and thus the weighted mean center based on population will be located closer to that area of the state.
Sources
Rogerson, P.A. (2015). Statistical methods for geography: A student's guide. Los Angeles, CA: Sage.Population 2000 and 2015 data provided by Dr. Ryan Weichelt of the University of Wisconsin- Eau Claire.
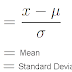


No comments:
Post a Comment