Introduction:
A foreclosure is the action of taking possession of a
mortgaged property when the mortgagor fails to keep up their mortgage payments (Weintraub, 2017).
Foreclosures are viewed as an indicator of economic decline, and are thus a
cause for worry among elected officials.
In Dane County, Wisconsin, county officials are concerned over their increase
in foreclosures from 2011 to 2012. Although
the reason behind the foreclosures cannot be determined, the spatial pattern of
foreclosures in the county and the likelihood foreclosures will increase in
2013 can be determined using basic statistics.
This report uses the number of foreclosures in 2011 and 2012 to explain
the pattern of foreclosures in Dane County and based on previous years’ data
determine the probability, or the likelihood of an increase in foreclosures in 2013.
Methodology:
The pattern of foreclosures from 2011 to 2012 was determined
by calculating the change from 2011 to 2012 and then based on that chang ecreating a map of standard
deviation in ArcMap. Standard deviation
is a statistic that describes how tightly the data clusters around the
mean, with large negative or positive
standard deviation values indicating the data point lies far from the mean.
First, the addresses of the foreclosures in 2011 and 2012 were geocoded, meaning x and y coordinates were attached to each address and mapped. Next they were added to the census tracts for Dane County. Then a new field was created in the attribute table subtracting the number of foreclosures in 2011 from the number of foreclosures in 2012. A standard deviation map was created from this field.
First, the addresses of the foreclosures in 2011 and 2012 were geocoded, meaning x and y coordinates were attached to each address and mapped. Next they were added to the census tracts for Dane County. Then a new field was created in the attribute table subtracting the number of foreclosures in 2011 from the number of foreclosures in 2012. A standard deviation map was created from this field.
To better understand the map and the data six z-scores were
calculated from three census tracts: 120.01, 108, and 25 with one in both 2011
and 2012 for each tract. Z-scores are standardized numbers from data values
converted by their relative position to the mean to allow comparison to a
normal or bell-shaped distribution curve. The mean, median, and standard
deviation for the whole county in 2011 and 2012 were obtained from the ArcGIS
software to calculate z-scores. The z-scores were
calculated using the formula below (Taylor, 2014).
 |
| Figure 1. Z-score formula. |
Finally, based on 2012 data, the number of foreclosures that
will be exceeded in 2013 80% and 10% of the time were calculated using the mean
and standard deviation obtained above and the appropriate z-scores from a z-score
and probability table. The calculations for all these steps is pictured below.
Results:
The map in figure 3 shows most census tracts seeing increases and decreases between 2.5 standard deviations from the mean.
 |
| Figure 3. Standard deviation map of the change in foreclosures from 2011 to 2012. |
However, census tracts 120.01, 116,
and 105.01 all had increases in foreclosures greater than 2.5 standard
deviations from the mean. In figure 3, a decrease in
foreclosures is indicated by the blue and green colors while an increase in
foreclosures is indicated by the orange and red colors. The map in figure 3
shows that most tracts in the center had very little change in foreclosures while
the outer ring of tracts showed more significant increases and decreases in
foreclosures. Census tract 120.01 had a z-score of 1.78 in 2011 but a
z-score of 3.0 in 2012. This increase is the most notable of the 3 census
tracts with calculated z-scores with a change of greater than 2.5 standard
deviations from the mean. Census tract 108 had z-scores of
2.01 and 1.48 in 2011 and 2012 and tract 25 had z-scores of -0.61 and -0.94 in
2011 and 2012 respectively. Both are shown in green in figure 3, which reflects
the decrease in foreclosures in both. However census tract 108 moved
closer to the mean in 2012 while tract 25 moved farther from the mean in
2012.
The final calculations determined
that 80% of the time approximately 4 foreclosures would be exceeded in Dane County while 10% of the time approximately 25 foreclosures would be exceeded in Dane county. These numbers are recorded in figure 2. Based on figure 3
and the number of foreclosures in 2012, the area that will exceed approximately
25 foreclosures will be the following census tracts: 120.01, 119, 116, 105.01,
118, and 30.01 all shown in figure 4. These tracts had an increase in
foreclosures from 2011 to 2012 and had at least 23 foreclosures in 2012.
 |
| Figure 4. Census tracts that will exceed 25 foreclosures. |
The area that will most likely
exceed approximately 4 foreclosures will be most of the map except for the
following census tracts: 25, 130, 17.05, 9.02, 101, 12, and 4.01. These
tracts, pictured in figure 5, all have less than four foreclosures in 2012 and
had a decrease in foreclosures from 2011 to 2012.
 |
| Figure 5. Census tracts that will not exceed four foreclosures. |
Finally, the mean and median
for 2011 were 11.39 and 11 respectively and 12.30 and 10 for 2012
respectively. These values indicate that in 2012 there was a large
outlier that influenced the mean in 2012 because the mean and median had a
difference of 2.3 while 2011 only had a difference of 0.39. This would
indicate that some county had a significant increase in foreclosures in 2012 from
2011. This finding supports the previous discussion on census tract
120.01 which showed dark red in figure 3 and had a large z-score in 2012.
Conclusions:
There were both increases and
decreases in foreclosures in Dane County from 2011 to 2012. Z-scores
calculated on three different census tracts mirrored the results in figure 3
and validated the data. Although county officials were concerned about
the increase in foreclosures from 2011 to 2012, only 60% of census tracts
showed an increase in foreclosures, while the rest saw none or a decrease in
the number of foreclosures. In addition, the mean number of foreclosures
from 2011 to 2012 went from 11.39 to 12.30, a 0.91 increase, not even by one
foreclosure. The median number of foreclosures actually decreased from
2011 to 2012, going from 11 to 10. This difference can be explained by
the previously mentioned 3 census tracts with an increase of foreclosures,
which increased the mean. These results indicate that although a slight
majority of census tracts saw an increase in foreclosures, the median number
went down (a number that isn’t influenced by large outliers) which indicates an
overall decreasing trend.
The results suggest than county
officials should focus their foreclosure reduction efforts in the counties with
a chance of exceeding 25 foreclosures shown in figure 4 because these counties
are at the most risk of continuing to see foreclosures as opposed to the previously
mentioned tracts that will not exceed even four. The median of 2011 and
2012 also suggest that foreclosures are not increasing for the whole county but
rather for a select few census tracts. More data is needed to determine
the cause of the spatial patterns. The general pattern that can be derived from figure 3 and the calculations suggests that the likelihood of an increase in foreclosures in 2013 is not equal for all census tracts. County officials should not be as concerned over the increases for the county and instead focus on decreasing the rate of foreclosures in the select counties that will likely see increases.
Sources:
Weintraub, E. (2017, February 26). What is a foreclosure: how do foreclosures work. Retrieved from https://www.thebalance.com/what-is-a-foreclosure-1798185Taylor, C. (2014, May 21). Z score formula. Retrieved from https://www.thoughtco.com/z-score-formula-3126281
Census tract and foreclosure data provided by Dr. Ryan Weichelt of the University of Wisconsin- Eau Claire.

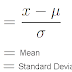


No comments:
Post a Comment